Цепенкова Ирина Павловна
Тема: Решение неравенств с одной переменной
Цель урока:
обобщить знания по теме "Решение неравенств с одной переменной"
Задачи:
обучающие:
- обобщить и систематизировать знания, полученные при изучении темы "Решение неравенств с одной переменной";
- рассмотреть решение неравенств с одной переменной различного вида;
- рассмотреть общие способы решения неравенств с одной переменной (метод последовательных упрощений, метод интервалов, метод замены переменной, функцинально-графический метод);
- закрепить умение применять основные теоремы равносильности при решении неравенств с одной переменной;
- способствовать расширению знаний по изучаемой теме;
развивающие:
- развитие логического мышления, памяти, умения рассуждать, исать рациональный способ решения поставленных задач;
- формирование умений сравнивать, обобщать, анализировать изучаемые факты;
- развитие у учащихся самостоятельности в мышлении и учебной деятельности;
- развитие математической речи;
воспитывающие:
- воспитание самоконтроля, ответственности, настойчивости в достижении поставленных целей;
- повышать уровень учебной мотивации с использованием компьютерных технологий;
- воспитание коллективизма, взаимопомощи и ответственности за общую работу;
- воспитание акуратности при выполнении практических заданий;
- воспитывать внимательность, активность, уверенность в себе.
Тип урока:
урок повторения и обобщения
Оборудование:
две ученических доски, интерактивная доска, проектор, компьютер
Программное обеспечение:
Microsoft Word, Microsoft PowePoint, 1C Математический конструктор 4.0, презентация к уроку
Учебник:
Алгебра и начала математического анализа. 11 класс. В 2 ч. Учебник для учащихся общеобразовательных учреждений (базовый уровень) / [А.Г. Мордкович и др.]; под ред. А.Г. Мордковича. - 4-е изд., стер. - М. : Мнемозина, 2013.
План урока:
1) организационный момент
2) повторение теоретических сведений по изучаемой теме
3) проверка домашнего задания, работа по карточкам
4) применение теоретических знаний на практике (решение задач устно и письменно по изучаемой теме)
5) самостоятельная работа
6) рефлексия
7) подведение итогов урока
8) запись домашнего задания
Ход урока
1) Организационный момент
Приветствие учащихся, проверка готовности к уроку, вступительное слово учителя, название темы, целей уроа, запись в тетрадях числа и темы урока
Слайд №1
 Ребята, на доске отображено множество различных неравенств. Какие неравенства вы видите?
Ребята, на доске отображено множество различных неравенств. Какие неравенства вы видите?
(Тригонометрические, иррациональные, степенные, линейные, квадратные, логарифмические, показательные, дробно-рациональные)
Что общего у этих неравенств?
(Все неравенства содержат одну переменную)
Начиная с восьмого класса вы изучаете решение таких неравенств. Сегодня на уроке мы поговорим о равносильности неравенств, применении теорем равносильности при их решении, а также вспомним основные методы решения неравенств с одной переменной. К концу урока пусть каждый из вас ответит на вопрос: "Насколько хорошо я владею тем или иным методом решения неравенств с одной переменной?"
Запишите в тетради число и тему урока "Решение неравенств с одной переменной"
2) Повторение теоретических сведений по изучаемой теме
Учитель выдает карточки с индивидуальными заданиями разного уровня сложности

Ответьте на вопрос: "Что называют решением неравенства?"
(Решением неравенства f(x) > g(x) называют всякое значение переменной x, которое обращает неравенство в верное числовое неравенство).
Слайд №2 (используется инструмент "шторка")
Рассмотрите пример. Назовите другие частные решения данного неравенства и числа, не являющиеся решением. Найдите общее решение данного неравенства. Что является общим решением неравенства с одной переменной?


Следующий вопрос: "Какие неравенства называются равносильными?"
(Неравенства f(x) > g(x) и p(x) > h(x) равносильны, если их решения совпадают)
Равносильны ли неравенства:
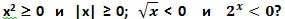
(Все неравенства решение которых множество действительных чисел - равносильны. Все неравенства решение которых пустое множество - равносильны).
Слайд №3 (используется инструмент "шторка")

Получить неравенство равносильное данному помогают теоремы равносильности. Повторим их и используем в решении неравенств устно.
Слайды №5 - 10 (используется инстумент "шторка")






Нам известны и ранее неоднократно при решении неравенств применялись четыре метода. Назовите их.
(Метод последовательных упрощений, метод интервалов, метод замены переменной, функционально-графический метод)
На эране вы видите четыре неравенства. Соотнесите каждое неравенство с соответствующим методом решения
Слайд №12

3) Проверка домашнего задания
Учащиеся поясняют свое решение

4) Применение теоретических знаний на практике
К доске вызываются три ученика. Двое работают самостоятельно. Решают №57.12б и неравенство
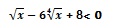
Один ученик работает вместе с классом (№57.10а). Затем у доски выполняется №57.30б и слушается ответ первых двух цчащихся.





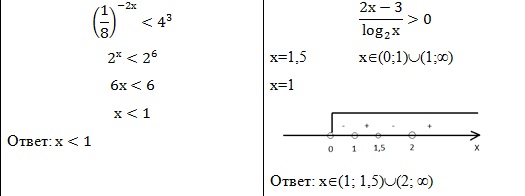
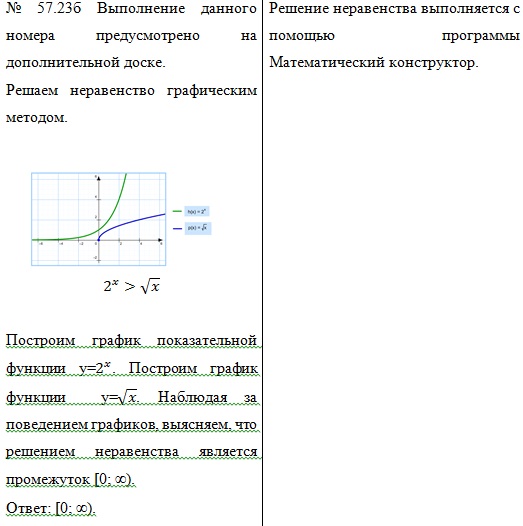
5) Самостоятельная работа по вариантам
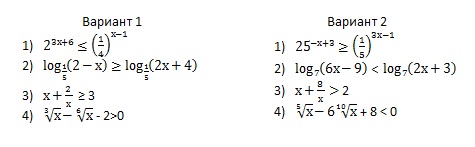
Проверка самостоятельной работы

Учащиеся проверяют ответы и оценивают свою работу. Правильно выполнено два задания - оценка "3", три задания - оценка "4", четыре задания - оценка "5".
6) Рефлексия
По итогам самостоятельной работы и всего урока учащиеся отвечают на вопрос, прозвучавший в начале урока: "Насколько хорошо я владею тем или иным методом решения неравенств с одной переменной?"
На обратной стороне листочка с самостоятельной работой содержится текст:

7) Итоги урока
Сегодня на уроке мы решали неравенства с одной переменной. С неравенствами каких видов мы работали? (Показательными, тригонометрическими, логарифмическими, рациональными, иррациональными, степенными)
Какие методы применяли при их решении? (Графический, метод интервалов, метод замены переменной, а таже применяли теоремы равносильности).
С какими трудностями вы столкнулись при решении неравенств с одной переменной?
Какие моменты в решении неравенств вам удавались успешнее всего?
Обсуждение трудностей и успехов.
Потренироваться в решении неравенств различного вида можно обратившись к следующему материалу:
Слайд №16
8) Записывается домашнее задание
№56.6б, 57.20б, 57.11б, 57.29б




